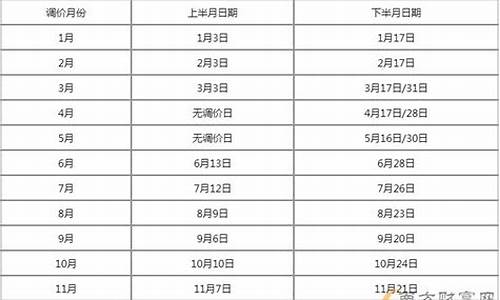
汽油调价最新消息和调整时间无锡_无锡汽油价格调整最新消息
1.一道数学问题(用一元一次方程或算术方法做)
2.由于国际原油价格持续上涨,国家发改委3月19日宣布,自3月20日零时起将汽、柴油价格每吨均提高600元.于
3.无锡夜间加油优惠时间价格及加油站
4.无锡夜间加油优惠时间价格和加油站
5.一元一次方程
6.初一解方程(50分悬赏分!!)

在一个方程中,如果只含有一个未知数,且未知数的最高次数是1的整式方程叫做一元一次方程。(linear equation in one)
一般形式:ax+b=0(a、b为常数,a≠0)。一元一次方程只有一个解。
一元一次方程的最终结果(方程的解)是x=a的形式
一元一次方程的“等式的性质1”和“等式的性质2”
1.等式两边同时加或减一个相同数,等式两边相等。(如果a=b,那么a±c=b±c。)
2.等式两边同时乘或除以一个相同数(0除外),或一个整式,等式两边相等。(如果a=b,那么ac=bc。如果a=b,c≠0,那么a/c=b/c。)
解法是通过移项将未知数移到一边,再把常数移到一边(等式基本性质1,注意符号!),然后两边同时除以未知数系数(化系数为1,等式基本性质2),即可得到未知数的值。
例:7x+23=100
解: 7x=100-23
7x=77
x=77÷7
x=11
在小学算术中,我们学习了用算术方法解决实际问题的有关知识,那么,一个实际问题能否应用一元一次方程来解决呢?若能解决,怎样解?用一元一次方程解应用题与用算术方法解应用题相比较,它有什么优越性呢?
为了回答上述这几个问题,我们来看下面这个例题.
例1 某数的3倍减2等于某数与4的和,求某数.
(首先,用算术方法解,由学生回答,教师板书)
解法1:(4+2)÷(3-1)=3.
答:某数为3.
(其次,用代数方法来解,教师引导,学生口述完成)
解法2:设某数为x,则有3x-2=x+4.
解之,得x=3.
答:某数为3.
纵观例1的这两种解法,很明显,算术方法不易思考,而应用设未知数,列出方程并通过解方程求得应用题的解的方法,有一种化难为易之感,这就是我们学习运用一元一次方程解应用题的目的之一.
我们知道方程是一个含有未知数的等式,而等式表示了一个相等关系.因此对于任何一个应用题中提供的条件,应首先从中找出一个相等关系,然后再将这个相等关系表示成方程.
简单的应用:求加数=和—另一个加数
求被减数=差+减数
求减数=被减数-差
求因数=积/另一个因数
求被除数=商*除数
求除数=被除数/商
一般解法:
⒈去分母 方程两边同时乘各分母的最小公倍数。
⒉去括号 一般先去小括号,在去中括号,最后去大括号。但顺序有时可依据情况而定使计算简便。可根据乘法分配律。
⒊移项 把方程中含有未知数的项移到方程的另一边,其余各项移到方程的另一边移项时别忘记了要变号。
⒋合并同类项 将原方程化为ax=b(a≠0)的形式。
⒌系数化1 方程两边同时除以未知数的系数,得出方程的解。
一元一次方程练习题
基本题型:
一、选择题:
1、下列各式中是一元一次方程的是( )
A. 5a+4b B.4x+9x
C. 5x2+9y2 D. 7a-4b
2、方程3x-2=-5(x-2)的解是( )
A.-1.5 B. 1.5C. 1 D. -1
3、若关于 的方程 的解满足方程 ,则 的值为( )
A. 10 B. 8 C. D.
4、下列根据等式的性质正确的是( )
A. 由 ,得 B. 由 ,得
C. 由 ,得 D. 由 ,得
5、解方程 时,去分母后,正确结果是( )
A. B.
C. C.
6 、电视机售价连续两次降价10%,降价后每台电视机的售价为a 元,则该电视机的原价为( )
A. 0.81a 元 B. 1.21a元 C. 1.1a元 D.0.1a 元
8、某商店卖出两件衣服,每件60元,其中一件赚25%,另一件亏25%,那么这两件衣服卖出后,商店是 ( )
A.不赚不亏 B.赚8元 C.亏8元 D. 赚8元
9、下列方程中,是一元一次方程的是( )
(A) (B) (C) (D)
10、方程 的解是( )
(A) (B) (C) (D)
11、已知等式 ,则下列等式中不一定成立的是( )
(A) (B)
(C) (D)
12、方程 的解是 ,则 等于( )
(A) (B) (C) (D)
13、解方程 ,去分母,得( )
(A) (B)
(C) (D)
14、下列方程变形中,正确的是( )
(A)方程 ,移项,得
(B)方程 ,去括号,得
(C)方程 ,未知数系数化为1,得
(D)方程 化成
15、儿子今年12岁,父亲今年39岁,( )父亲的年龄是儿子的年龄的4倍.
(A)3年后; (B)3年前; (C)9年后; (D)不可能.
16、重庆力帆新感觉足球队训练用的足球是由32块黑白相间的牛皮缝制而成的,其中黑皮可看作正五边形,白皮可看作正六边形,黑、白皮块的数目比为3:5,要求出黑皮、白皮的块数,若设黑皮的块数为 ,则列出的方程正确的是( )
(A) (B)
(C) (D)
17、珊瑚中学修建综合楼后,剩有一块长比宽多5m、周长为50m的长方形空地. 为了美化环境,学校决定将它种植成草皮,已知每平方米草皮的种植成本最低是 元,那么种植草皮至少需用( )
(A) 元; (B) 元; (C) 元; (D) 元.
一年期 二年期 三年期
2.25 2.43 2.70
18、银行教育储蓄的年利率如右下表:
小明现正读七年级,今年7月他父母为他在银行存款30000元,以供3年后上高中使用. 要使3年后的收益最大,则小明的父母应该用( )
(A)直接存一个3年期;
(B)先存一个1年期的,1年后将利息和自动转存一个2年期;
(C)先存一个1年期的,1年后将利息和自动转存两个1年期;
(D)先存一个2年期的,2年后将利息和自动转存一个1年期.
二. 填空题:
1、 ,则 ________.
2、已知 ,则 __________.
3、关于 的方程 的解是3,则 的值为________________.
4、现有一个三位数,其个位数为 ,十位上的数字为 ,百位数上的数字为 ,则这个三位数表示为__________________.
5、甲、乙两班共有学生96名,甲班比乙班多2人,则乙班有____________人.
6、某数的3倍比它的一半大2,若设某数为 ,则列方程为____.
7、当 ___时,代数式 与 的值互为相反数.
8、在公式 中,已知 ,则 ___.
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
9、如右图是2003年12月份的日历,现用一长方形在日历中任意框出4个数
,请用一个等式表示 之间的关系______________.
10、一根内径为3㎝的圆柱形长试管中装满了水,现把试管中的水逐渐滴入一个内径为8㎝、高为1.8㎝的圆柱形玻璃杯中,当玻璃杯装满水时,试管中的水的高度下降了____㎝.
11、国庆期间,“新世纪百货”搞换季打折. 简爽同学以8折的优惠价购买了一件运动服节省16元,那么他购买这件衣服实际用了___元.
12、成渝铁路全长504千米. 一辆快车以90千米/时的速度从重庆出发,1小时后,另有一辆慢车以48千米/时的速度从成都出发,则慢车出发__小时后两车相遇(沿途各车站的停留时间不计).
13、我们小时候听过龟兔赛跑的故事,都知道乌龟最后战胜了小白兔. 如果在第二次赛跑中,小白兔知耻而后勇,在落后乌龟1千米时,以101米/分的速度奋起直追,而乌龟仍然以1米/分的速度爬行,那么小白兔大概需要___分钟就能追上乌龟.
14、一年定期存款的年利率为1.98%,到期取款时须扣除利息的20%作为利息税上缴国库. 若小颖存一笔一年定期储蓄,到期扣除利息税后实得利息158.4元,那么她存入的人民币是____元
15、52辆车排成两队,每辆车长a米,前后两车间隔3a/2米,车队平均每分钟行50米,这列车队通过长为546米的广场需要的时间是16分钟,则a=__________.
三、解方程:
1、 2、
3、 4、
5、 6、
7、 8、
9、已知 是方程 的根,求代数式 的值.
四、列方程解应用题:
1、敌军在离我军8千米的驻地逃跑,时间是早晨4点,我军于5点出发以每小时10千米的速度追击,结果在7点追上.求敌军逃跑时的速度是多少?
2、期中考查,信息技术课老师限时40分钟要求每位七年级学生打完一篇文章. 已知独立打完同样大小文章,小宝需要50分钟,小贝只需要30分钟. 为了完成任务,小宝打了30分钟后,请求小贝帮助合作,他能在要求的时间打完吗?
3、在学完“有理数的运算”后,实验中学七年级各班各选出5名学生组成一个代表队,在数学方老师的组织下进行一次知识竞赛. 竞赛规则是:每队都分别给出50道题,答对一题得3分,⑴ 如果二班代表队最后得分142分,那么二班代表队回答对了多少道题?⑵ 一班代表队的最后得分能为145分吗?请简要说明理由.
4、某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门). 安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%. 安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离. 设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
5、黑熊妈妈想检测小熊学习“列方程解应用题”的效果,给了小熊19个苹果,要小熊把它们分成4堆. 要求分后,如果再把第一堆增加一倍,第二堆增加一个,第三堆减少两个,第四堆减少一倍后,这4堆苹果的个数又要相同. 小熊捎捎脑袋,该如何分这19个苹果为4堆呢?
6、学校准备拿出2000元资金给22名“希望杯”竞赛获奖学生买奖品,一等奖每人200元奖品,二等奖每人50元奖品,求得到一等奖和二等奖的学生分别是多少人?
7、一家商店将某种商品按成本价提高40%后标价,元旦期间,欲打八折销售,以答谢新老顾客对本商厦的光顾,售价为224元,这件商品的成本价是多少元?
8、甲乙两人从学校到1000米远的展览馆去参观,甲走了5分钟后乙才出发,甲的速度是80米/分,乙的速度是180米/分,问乙多长时间能追上甲?追上甲时离展览馆还有多远?
较高要求:
1、已知 ,那么代数式 的值。
2、(2001年江苏省无锡市中考题)某商场根据市场信息,对商场中现有的两台不同型号的空调进行调价销售,其中一台空调调价后售出可获利10%(相对于进价),另一台空调调价后售出则亏本10%(相对于进价),而这两台空调调价后的售价恰好相同,那么商场把这两台空调调价后售出( ).
(A)既不获利也不亏本 (B)可获利1% (C)要亏本2% (D)要亏本1%
3、某开发商按照分期付款的形式售房,小明家购买了一价为12万元的新房,购房时需首付(第一年)款3万元,从第二年起,以后每年应付房款为5000元与上一年剩余欠款的利息之和。已知剩余款的年利率为0.4%,问第几年小明家需交房款5200元?
4、某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元;若制成奶片销售,每吨可获利润2000元.
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成;
(1)你认为选择哪种方案获利最多,为什么?
(2)本题解出之后,你还能提出哪些问题?若没解出,写出你存在的问题?
5、两辆汽车从同一地点同时出发,沿着同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油。为了使其中一车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里地方返回?离出发地点最远的那辆车一共行驶了多少公里?
一道数学问题(用一元一次方程或算术方法做)
一元一次方程练习题
基本题型:
一、选择题:
1、下列各式中是一元一次方程的是( )
A. B.
C. D.
2、方程 的解是( )
A. B. C. 1 D. -1
3、若关于 的方程 的解满足方程 ,则 的值为( )
A. 10 B. 8 C. D.
4、下列根据等式的性质正确的是( )
A. 由 ,得 B. 由 ,得
C. 由 ,得 D. 由 ,得
5、解方程 时,去分母后,正确结果是( )
A. B.
C. C.
6、电视机售价连续两次降价10%,降价后每台电视机的售价为a 元,则该电视机的原价为( )
A. 0.81a 元 B. 1.21a元 C. 元 D. 元
8、某商店卖出两件衣服,每件60元,其中一件赚25%,另一件亏25%,那么这两件衣服卖出后,商店是 ( )
A.不赚不亏 B.赚8元 C.亏8元 D. 赚8元
9、下列方程中,是一元一次方程的是( )
(A) (B) (C) (D)
10、方程 的解是( )
(A) (B) (C) (D)
11、已知等式 ,则下列等式中不一定成立的是( )
(A) (B)
(C) (D)
12、方程 的解是 ,则 等于( )
(A) (B) (C) (D)
13、解方程 ,去分母,得( )
(A) (B)
(C) (D)
14、下列方程变形中,正确的是( )
(A)方程 ,移项,得
(B)方程 ,去括号,得
(C)方程 ,未知数系数化为1,得
(D)方程 化成
15、儿子今年12岁,父亲今年39岁,( )父亲的年龄是儿子的年龄的4倍.
(A)3年后; (B)3年前; (C)9年后; (D)不可能.
16、重庆力帆新感觉足球队训练用的足球是由32块黑白相间的牛皮缝制而成的,其中黑皮可看作正五边形,白皮可看作正六边形,黑、白皮块的数目比为3:5,要求出黑皮、白皮的块数,若设黑皮的块数为 ,则列出的方程正确的是( )
(A) (B)
(C) (D)
17、珊瑚中学修建综合楼后,剩有一块长比宽多5m、周长为50m的长方形空地. 为了美化环境,学校决定将它种植成草皮,已知每平方米草皮的种植成本最低是 元,那么种植草皮至少需用( )
(A) 元; (B) 元; (C) 元; (D) 元.
一年期 二年期 三年期
2.25 2.43 2.70
18、银行教育储蓄的年利率如右下表:
小明现正读七年级,今年7月他父母为他在银行存款30000元,以供3年后上高中使用. 要使3年后的收益最大,则小明的父母应该用( )
(A)直接存一个3年期;
(B)先存一个1年期的,1年后将利息和自动转存一个2年期;
(C)先存一个1年期的,1年后将利息和自动转存两个1年期;
(D)先存一个2年期的,2年后将利息和自动转存一个1年期.
二. 填空题:
1、 ,则 ________.
2、已知 ,则 __________.
3、关于 的方程 的解是3,则 的值为________________.
4、现有一个三位数,其个位数为 ,十位上的数字为 ,百位数上的数字为 ,则这个三位数表示为__________________.
5、甲、乙两班共有学生96名,甲班比乙班多2人,则乙班有____________人.
6、某数的3倍比它的一半大2,若设某数为 ,则列方程为____.
7、当 ___时,代数式 与 的值互为相反数.
8、在公式 中,已知 ,则 ___.
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
9、如右图是2003年12月份的日历,现用一长方形在日历中任意框出4个数
,请用一个等式表示 之间的关系______________.
10、一根内径为3㎝的圆柱形长试管中装满了水,现把试管中的水逐渐滴入一个内径为8㎝、高为1.8㎝的圆柱形玻璃杯中,当玻璃杯装满水时,试管中的水的高度下降了____㎝.
11、国庆期间,“新世纪百货”搞换季打折. 简爽同学以8折的优惠价购买了一件运动服节省16元,那么他购买这件衣服实际用了___元.
12、成渝铁路全长504千米. 一辆快车以90千米/时的速度从重庆出发,1小时后,另有一辆慢车以48千米/时的速度从成都出发,则慢车出发__小时后两车相遇(沿途各车站的停留时间不计).
13、我们小时候听过龟兔赛跑的故事,都知道乌龟最后战胜了小白兔. 如果在第二次赛跑中,小白兔知耻而后勇,在落后乌龟1千米时,以101米/分的速度奋起直追,而乌龟仍然以1米/分的速度爬行,那么小白兔大概需要___分钟就能追上乌龟.
14、一年定期存款的年利率为1.98%,到期取款时须扣除利息的20%作为利息税上缴国库. 若小颖存一笔一年定期储蓄,到期扣除利息税后实得利息158.4元,那么她存入的人民币是____元
15、52辆车排成两队,每辆车长a米,前后两车间隔3a/2米,车队平均每分钟行50米,这列车队通过长为546米的广场需要的时间是16分钟,则a=__________.
三、解方程:
1、 2、
3、 4、
5、 6、
7、 8、
9、已知 是方程 的根,求代数式 的值.
四、列方程解应用题:
1、敌军在离我军8千米的驻地逃跑,时间是早晨4点,我军于5点出发以每小时10千米的速度追击,结果在7点追上.求敌军逃跑时的速度是多少?
2、期中考查,信息技术课老师限时40分钟要求每位七年级学生打完一篇文章. 已知独立打完同样大小文章,小宝需要50分钟,小贝只需要30分钟. 为了完成任务,小宝打了30分钟后,请求小贝帮助合作,他能在要求的时间打完吗?
3、在学完“有理数的运算”后,实验中学七年级各班各选出5名学生组成一个代表队,在数学方老师的组织下进行一次知识竞赛. 竞赛规则是:每队都分别给出50道题,答对一题得3分,⑴ 如果二班代表队最后得分142分,那么二班代表队回答对了多少道题?⑵ 一班代表队的最后得分能为145分吗?请简要说明理由.
4、某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门). 安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%. 安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离. 设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
5、黑熊妈妈想检测小熊学习“列方程解应用题”的效果,给了小熊19个苹果,要小熊把它们分成4堆. 要求分后,如果再把第一堆增加一倍,第二堆增加一个,第三堆减少两个,第四堆减少一倍后,这4堆苹果的个数又要相同. 小熊捎捎脑袋,该如何分这19个苹果为4堆呢?
6、学校准备拿出2000元资金给22名“希望杯”竞赛获奖学生买奖品,一等奖每人200元奖品,二等奖每人50元奖品,求得到一等奖和二等奖的学生分别是多少人?
7、一家商店将某种商品按成本价提高40%后标价,元旦期间,欲打八折销售,以答谢新老顾客对本商厦的光顾,售价为224元,这件商品的成本价是多少元?
8、甲乙两人从学校到1000米远的展览馆去参观,甲走了5分钟后乙才出发,甲的速度是80米/分,乙的速度是180米/分,问乙多长时间能追上甲?追上甲时离展览馆还有多远?
较高要求:
1、已知 ,那么代数式 的值。
2、(2001年江苏省无锡市中考题)某商场根据市场信息,对商场中现有的两台不同型号的空调进行调价销售,其中一台空调调价后售出可获利10%(相对于进价),另一台空调调价后售出则亏本10%(相对于进价),而这两台空调调价后的售价恰好相同,那么商场把这两台空调调价后售出( ).
(A)既不获利也不亏本 (B)可获利1% (C)要亏本2% (D)要亏本1%
3、某开发商按照分期付款的形式售房,小明家购买了一价为12万元的新房,购房时需首付(第一年)款3万元,从第二年起,以后每年应付房款为5000元与上一年剩余欠款的利息之和。已知剩余款的年利率为0.4%,问第几年小明家需交房款5200元?
4、某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元;若制成奶片销售,每吨可获利润2000元.
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成;
(1)你认为选择哪种方案获利最多,为什么?
(2)本题解出之后,你还能提出哪些问题?若没解出,写出你存在的问题?
5、两辆汽车从同一地点同时出发,沿着同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油。为了使其中一车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里地方返回?离出发地点最远的那辆车一共行驶了多少公里?
由于国际原油价格持续上涨,国家发改委3月19日宣布,自3月20日零时起将汽、柴油价格每吨均提高600元.于
解:因为摩托车有2个轮子,三轮车有3个轮子,小轿车有4个轮子,共有15只轮子,故三轮车只能是1辆或3辆,因为如果是2、4辆,则轮子数是偶数
(1)当三轮车是1辆时,摩托车、小轿车共5辆, 共有12只轮子
算术:摩托车:(4×5-12)÷(4-2)=4(辆)
小轿车:5-4=1(辆)
方程:设摩托车x辆,则小轿车(5-x)辆
2x+4(5-x)=12
x=4 5-x=1
(2) 当三轮车是3辆时,摩托车、小轿车共3辆, 共有6只轮子
则:摩托车3辆,没有小轿车(不合题意,舍去)
故:三轮车1辆,摩托车4辆,小轿车1辆
无锡夜间加油优惠时间价格及加油站
(1)∵每次都加50升93号汽油,调价后加一次油比调价前要多花23.5元,
∴每升汽油提高了:23.5÷50=0.47(元),
∵江苏省内93号汽油在原来每升7.45元,
∴3月20日零时起江苏省内93号汽油价格调整为每升:7.45+0.47=7.92元;
(2)设老李现在每次固定的加油金额至少为x元,
根据题意得出:
| x |
| 7.92 |
| x |
| 8.25 |
解得:x≥2,
∵精确到10元,∴x≥300,
答:老李现在每次固定的加油金额至少为300元.
无锡夜间加油优惠时间价格和加油站
无锡近期多个地方晚上加油会有优惠,所以小伙伴们如果对这方面感兴趣可以详细了解一下,大家要注意只有在特定的时间前往瑷珲有优惠,下面就一起看看详细优惠信息。
中石油夜间错峰加油优惠
为了促进夜间加油和消费,即日起晚上8点至次日6点,中石油无锡区域在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:7月至9月晚8点-早6点
二、活动内容:
1.指定加油站晚20:00至早6:00期间,汽油客户(网约车客户不参加通过现场扫码参与汽油消费满200元立减5元活动,优惠幅度2.5%。
2.网约车客户在晚20:00至早6:00期间,单次加油满200元赠送非油爆款商品(具体商品以加油站为准。
3.具备洗车条件的高田、黄田港加油站,晚20:00至早6:00期间,消费汽油满100元赠送洗车一次。
三、活动站点:
中石化夜间错峰加油优惠
无锡区域
为了促进夜间加油和消费,即日起晚上8点至次日6点,中石化无锡区域在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:每日晚20:00至次日6:00
二、活动内容:
1.使用“加油江苏”APP一键加油功能的客户,夜间在城区指定加油站加油,可享受2%优惠
2.网约车认证客户在我司自营站点加汽油,享受0.3元/升的优惠。
3.个人会员客户在我司指定站点加油、购物,享受双倍会员积分返还。
三、优惠加油活动站点:
一、活动时间:每日晚20:00至次日6:00
二、活动内容:会员客户,夜间在城区指定站点加上,持卡加油满额送免费洗车券一张。
三、免费洗车活动站点:
江阴区域
为了促进夜间加油和消费,即日起晚上8点至次日6点,中石化江阴区域在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:20点至次日6点
二、活动内容:
1.电子钱包一键加油客户:
晚8点至次日早6点,客户在我司上述指定站点使用加油江苏APP一键加油功能加汽油任意金额立减2%。
2.网约车持卡客户:
晚8点至次日早6点,网约车认证客户在我司自营站点加汽油,享受0.3元/升的优惠。
3.加油购物双倍积分:
晚8点至次日早6点,个人会员客户在我司上述指定站点加油、购物,享双倍会员积分返还。
三、活动站点:
中石化壳牌夜间错峰加油优惠
为了促进夜间加油和消费,即日起晚上8点至次日6点,中石化壳牌无锡区域在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:20点至次日6点
二、活动内容:
1.电子钱包一键加油客户:
晚8点至次日早6点,客户在我司上述指定站点使用加油江苏APP一键加油功能加汽油任意金额立减2%。
2.网约车持卡客户:
晚8点至次日早6点,网约车认证客户在我司自营站点加汽油,享受0.3元/升的优惠。
3.加油购物双倍积分:
晚8点至次日早6点,个人会员客户在我司上述指定站点加油、
购物,享双倍会员积分返还。
三、活动站点:
中海油夜间错峰加油优惠
为了促进夜间加油和消费,即日起晚上8点至次日6点,中海油无锡区域在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:20点至次日6点
二、活动内容:
分两个阶段:第一阶段是7月24-7月31日,客户充值1000返利20元油品券(夜间使用;第二阶段是8月1日—9月20日,每个客户都可以在公众号(海油行线上领取2元和5元的电子券,满100减2元满200减5元(夜间使用
三、活动站点:
一元一次方程
最近无锡很多地方晚上加油都会有优惠,对这方面感兴趣的朋友可以多了解一下。一定时间去爱辉要注意优惠。下面我们来看看详细的优惠信息。
中石油夜间错峰加油优惠
为促进夜间加油消费,晚上8:00-次日6:00,中石油无锡地区将在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:7-9月晚8点-早6点
二。活动:
1.在晚上20:00至早上6:00期间,在指定加油站,汽油客户(未参与网上叫车服务的客户)通过现场扫码参与汽油消费立减200元、立减5元的活动,优惠幅度为2.5%。
2.网约车客户在晚上20:00-早上6:00期间,加满200元加油,赠送非油爆品(具体商品以加油站为准)。
3.在具备洗车条件的高田、黄田岗加油站,晚上20:00-早上6:00,100元送一次洗车。
三、活动现场:
中石化夜间错峰加油优惠
无锡地区
为促进夜间加油和消费,晚上8:00至次日6:00,中石化无锡地区将在上述指定油站开展夜间非高峰加油优惠活动。
一、活动时间:每晚20:00至次日6:00。
二。活动:
1.使用“加油江苏”APP一键加油功能的客户,夜间在市区指定加油站加油,可享受2%的优惠。
2.通过网约车服务认证的客户,在我们的自营站点加油,可以获得0.3元/升的优惠。
3.个人会员客户可在我公司指定站点加油购物,享受双倍会员积分返还。
三、优惠加油活动现场:
一、活动时间:每晚20:00至次日6:00。
二。活动内容:会员和客户,晚上在市内指定站点添加,可获得免费洗车券,满卡加油。
三、免费洗车活动现场:
江阴地区
为促进夜间加油消费,晚8:00-次日6:00,中石化江阴地区将在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:20:00至次日6:00
二。活动:
1.电子钱包一键加油客户:
晚上8:00至次日早上6:00,客户在我公司上述指定站点使用‘加油江苏’APP的一键加油功能,任意量汽油立减2%。
2.在线汽车持卡人:
晚上8点到早上6点,网约车服务认证客户到我们自营站点加油,享受0.3元/升的优惠。
3.加油购物双倍积分:
个人会员客户晚8:00至次日早6:00在我公司上述指定站点加油、购物,享受双倍会员积分。
三、活动现场:
中石化壳牌夜间错峰加油优惠
为促进夜间加油消费,晚上8:00-次日6:00,中石化壳牌无锡地区将在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:20:00至次日6:00
二。活动:
1.电子钱包一键加油客户:
晚上8:00至次日早上6:00,客户在我公司上述指定站点使用‘加油江苏’APP的一键加油功能,任意量汽油立减2%。
2.在线汽车持卡人:
晚上8点到早上6点,网约车服务认证客户到我们自营站点加油,享受0.3元/升的优惠。
3.加油购物双倍积分:
个人会员客户在晚8:00至次日早6:00在我公司上述指定地点加油,
购物,享受双倍会员积分返还。
三、活动现场:
中海油夜间错峰加油优惠
为促进夜间加油消费,晚上8:00-次日6:00,中海油无锡地区将在上述指定油站开展夜间错峰加油优惠活动。
一、活动时间:20:00至次日6:00
二。活动:
分两个阶段:第一阶段为7月24日至7月31日,客户充值1000张20元油券(夜间使用);第二阶段为8月1日至9月20日。E
初一解方程(50分悬赏分!!)
一元一次方程 在一个方程中,如果只含有一个未知数,且未知数的最高次数是1的整式方程叫做一元一次方程。(linear equation in one)
一般形式:ax+b=0(a、b为常数,a≠0)。一元一次方程只有一个解。
一元一次方程的最终结果(方程的解)是x=a的形式
一元一次方程的“等式的性质1”和“等式的性质2”
1.等式两边同时加或减一个相同数,等式两边相等。(如果a=b,那么a±c=b±c。)
2.等式两边同时乘或除以一个相同数(0除外),或一个整式,等式两边相等。(如果a=b,那么ac=bc。如果a=b,c≠0,那么a/c=b/c。)
解法是通过移项将未知数移到一边,再把常数移到一边(等式基本性质1,注意符号!),然后两边同时除以未知数系数(化系数为1,等式基本性质2),即可得到未知数的值。
例:7x+23=100
解: 7x=100-23
7x=77
x=77÷7
x=11
在小学算术中,我们学习了用算术方法解决实际问题的有关知识,那么,一个实际问题能否应用一元一次方程来解决呢?若能解决,怎样解?用一元一次方程解应用题与用算术方法解应用题相比较,它有什么优越性呢?
为了回答上述这几个问题,我们来看下面这个例题.
例1 某数的3倍减2等于某数与4的和,求某数.
(首先,用算术方法解,由学生回答,教师板书)
解法1:(4+2)÷(3-1)=3.
答:某数为3.
(其次,用代数方法来解,教师引导,学生口述完成)
解法2:设某数为x,则有3x-2=x+4.
解之,得x=3.
答:某数为3.
纵观例1的这两种解法,很明显,算术方法不易思考,而应用设未知数,列出方程并通过解方程求得应用题的解的方法,有一种化难为易之感,这就是我们学习运用一元一次方程解应用题的目的之一.
我们知道方程是一个含有未知数的等式,而等式表示了一个相等关系.因此对于任何一个应用题中提供的条件,应首先从中找出一个相等关系,然后再将这个相等关系表示成方程.
简单的应用:求加数=和—另一个加数
求被减数=差+减数
求减数=被减数-差
求因数=积/另一个因数
求被除数=商*除数
求除数=被除数/商
一般解法:
⒈去分母 方程两边同时乘各分母的最小公倍数。
⒉去括号 一般先去小括号,在去中括号,最后去大括号。但顺序有时可依据情况而定使计算简便。可根据乘法分配律。
⒊移项 把方程中含有未知数的项移到方程的另一边,其余各项移到方程的另一边移项时别忘记了要变号。
⒋合并同类项 将原方程化为ax=b(a≠0)的形式。
⒌系数化1 方程两边同时除以未知数的系数,得出方程的解。
一元一次方程练习题
基本题型:
一、选择题:
1、下列各式中是一元一次方程的是( )
A. 5a+4b B.4x+9x
C. 5x2+9y2 D. 7a-4b
2、方程3x-2=-5(x-2)的解是( )
A.-1.5 B. 1.5C. 1 D. -1
3、若关于 的方程 的解满足方程 ,则 的值为( )
A. 10 B. 8 C. D.
4、下列根据等式的性质正确的是( )
A. 由 ,得 B. 由 ,得
C. 由 ,得 D. 由 ,得
5、解方程 时,去分母后,正确结果是( )
A. B.
C. C.
6 、电视机售价连续两次降价10%,降价后每台电视机的售价为a 元,则该电视机的原价为( )
A. 0.81a 元 B. 1.21a元 C. 1.1a元 D.0.1a 元
8、某商店卖出两件衣服,每件60元,其中一件赚25%,另一件亏25%,那么这两件衣服卖出后,商店是 ( )
A.不赚不亏 B.赚8元 C.亏8元 D. 赚8元
9、下列方程中,是一元一次方程的是( )
(A) (B) (C) (D)
10、方程 的解是( )
(A) (B) (C) (D)
11、已知等式 ,则下列等式中不一定成立的是( )
(A) (B)
(C) (D)
12、方程 的解是 ,则 等于( )
(A) (B) (C) (D)
13、解方程 ,去分母,得( )
(A) (B)
(C) (D)
14、下列方程变形中,正确的是( )
(A)方程 ,移项,得
(B)方程 ,去括号,得
(C)方程 ,未知数系数化为1,得
(D)方程 化成
15、儿子今年12岁,父亲今年39岁,( )父亲的年龄是儿子的年龄的4倍.
(A)3年后; (B)3年前; (C)9年后; (D)不可能.
16、重庆力帆新感觉足球队训练用的足球是由32块黑白相间的牛皮缝制而成的,其中黑皮可看作正五边形,白皮可看作正六边形,黑、白皮块的数目比为3:5,要求出黑皮、白皮的块数,若设黑皮的块数为 ,则列出的方程正确的是( )
(A) (B)
(C) (D)
17、珊瑚中学修建综合楼后,剩有一块长比宽多5m、周长为50m的长方形空地. 为了美化环境,学校决定将它种植成草皮,已知每平方米草皮的种植成本最低是 元,那么种植草皮至少需用( )
(A) 元; (B) 元; (C) 元; (D) 元.
一年期 二年期 三年期
2.25 2.43 2.70
18、银行教育储蓄的年利率如右下表:
小明现正读七年级,今年7月他父母为他在银行存款30000元,以供3年后上高中使用. 要使3年后的收益最大,则小明的父母应该用( )
(A)直接存一个3年期;
(B)先存一个1年期的,1年后将利息和自动转存一个2年期;
(C)先存一个1年期的,1年后将利息和自动转存两个1年期;
(D)先存一个2年期的,2年后将利息和自动转存一个1年期.
二. 填空题:
1、 ,则 ________.
2、已知 ,则 __________.
3、关于 的方程 的解是3,则 的值为________________.
4、现有一个三位数,其个位数为 ,十位上的数字为 ,百位数上的数字为 ,则这个三位数表示为__________________.
5、甲、乙两班共有学生96名,甲班比乙班多2人,则乙班有____________人.
6、某数的3倍比它的一半大2,若设某数为 ,则列方程为____.
7、当 ___时,代数式 与 的值互为相反数.
8、在公式 中,已知 ,则 ___.
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
9、如右图是2003年12月份的日历,现用一长方形在日历中任意框出4个数
,请用一个等式表示 之间的关系______________.
10、一根内径为3㎝的圆柱形长试管中装满了水,现把试管中的水逐渐滴入一个内径为8㎝、高为1.8㎝的圆柱形玻璃杯中,当玻璃杯装满水时,试管中的水的高度下降了____㎝.
11、国庆期间,“新世纪百货”搞换季打折. 简爽同学以8折的优惠价购买了一件运动服节省16元,那么他购买这件衣服实际用了___元.
12、成渝铁路全长504千米. 一辆快车以90千米/时的速度从重庆出发,1小时后,另有一辆慢车以48千米/时的速度从成都出发,则慢车出发__小时后两车相遇(沿途各车站的停留时间不计).
13、我们小时候听过龟兔赛跑的故事,都知道乌龟最后战胜了小白兔. 如果在第二次赛跑中,小白兔知耻而后勇,在落后乌龟1千米时,以101米/分的速度奋起直追,而乌龟仍然以1米/分的速度爬行,那么小白兔大概需要___分钟就能追上乌龟.
14、一年定期存款的年利率为1.98%,到期取款时须扣除利息的20%作为利息税上缴国库. 若小颖存一笔一年定期储蓄,到期扣除利息税后实得利息158.4元,那么她存入的人民币是____元
15、52辆车排成两队,每辆车长a米,前后两车间隔3a/2米,车队平均每分钟行50米,这列车队通过长为546米的广场需要的时间是16分钟,则a=__________.
三、解方程:
1、 2、
3、 4、
5、 6、
7、 8、
9、已知 是方程 的根,求代数式 的值.
四、列方程解应用题:
1、敌军在离我军8千米的驻地逃跑,时间是早晨4点,我军于5点出发以每小时10千米的速度追击,结果在7点追上.求敌军逃跑时的速度是多少?
2、期中考查,信息技术课老师限时40分钟要求每位七年级学生打完一篇文章. 已知独立打完同样大小文章,小宝需要50分钟,小贝只需要30分钟. 为了完成任务,小宝打了30分钟后,请求小贝帮助合作,他能在要求的时间打完吗?
3、在学完“有理数的运算”后,实验中学七年级各班各选出5名学生组成一个代表队,在数学方老师的组织下进行一次知识竞赛. 竞赛规则是:每队都分别给出50道题,答对一题得3分,⑴ 如果二班代表队最后得分142分,那么二班代表队回答对了多少道题?⑵ 一班代表队的最后得分能为145分吗?请简要说明理由.
4、某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门). 安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%. 安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离. 设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
5、黑熊妈妈想检测小熊学习“列方程解应用题”的效果,给了小熊19个苹果,要小熊把它们分成4堆. 要求分后,如果再把第一堆增加一倍,第二堆增加一个,第三堆减少两个,第四堆减少一倍后,这4堆苹果的个数又要相同. 小熊捎捎脑袋,该如何分这19个苹果为4堆呢?
6、学校准备拿出2000元资金给22名“希望杯”竞赛获奖学生买奖品,一等奖每人200元奖品,二等奖每人50元奖品,求得到一等奖和二等奖的学生分别是多少人?
7、一家商店将某种商品按成本价提高40%后标价,元旦期间,欲打八折销售,以答谢新老顾客对本商厦的光顾,售价为224元,这件商品的成本价是多少元?
8、甲乙两人从学校到1000米远的展览馆去参观,甲走了5分钟后乙才出发,甲的速度是80米/分,乙的速度是180米/分,问乙多长时间能追上甲?追上甲时离展览馆还有多远?
较高要求:
1、已知 ,那么代数式 的值。
2、(2001年江苏省无锡市中考题)某商场根据市场信息,对商场中现有的两台不同型号的空调进行调价销售,其中一台空调调价后售出可获利10%(相对于进价),另一台空调调价后售出则亏本10%(相对于进价),而这两台空调调价后的售价恰好相同,那么商场把这两台空调调价后售出( ).
(A)既不获利也不亏本 (B)可获利1% (C)要亏本2% (D)要亏本1%
3、某开发商按照分期付款的形式售房,小明家购买了一价为12万元的新房,购房时需首付(第一年)款3万元,从第二年起,以后每年应付房款为5000元与上一年剩余欠款的利息之和。已知剩余款的年利率为0.4%,问第几年小明家需交房款5200元?
4、某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元;若制成奶片销售,每吨可获利润2000元.
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成;
(1)你认为选择哪种方案获利最多,为什么?
(2)本题解出之后,你还能提出哪些问题?若没解出,写出你存在的问题?
5、两辆汽车从同一地点同时出发,沿着同一方向同速直线行驶,每车最多只能带24桶汽油,途中不能用别的油,每桶油可使一辆车前进60公里,两车都必须返回出发地点,但是可以不同时返回,两车相互可借用对方的油。为了使其中一车尽可能地远离出发地点,另一辆车应当在离出发地点多少公里地方返回?离出发地点最远的那辆车一共行驶了多少公里?
1.(x-1.5-1)/4=(x-1.5+1)/5
5(x-2.5)=4(x-0.5)
x=-2+12.5
x=10.5
2.l+300=30v
300-l=10v
v=15m/s
l=150m
3.80x+80y=400
80y-80x=400
所以x=0 y=5
4.[x-4*(18-x-y)/60]/4=(18-y)/60
y/4=(18-x)/60+(18-x-y)/60
所以x=2 y=2
5.x=4y
3x+11-x-y=25
x=8
y=2
6.(x-2)12=8x
x=6
7.x+y=4/5.2
x-y=4/6.5
解得:x=9/13,y=1/13
8.5*(1/3)+5*X=15*X
x=1/6
9.(1/3)x/12=(1/3)x/[12*(5/4)]+1
化简得:
(5/3)x=(4/3)x+60
(1/3)x=60
x=180
10.2X+5X=14000
7X=14000
X=2000
2X=4000
5X=10000
11. x+(35-20)*1.5%x=1323 x=1080
12 . 2x-10.3x=15
13 . 0.52x-(1-0.52)x=80
14 . x/2+3x/2=7
15 . 3x+7=32-2x
16 . 3x+5(138-x)=540
17 . 3x-7(x-1)=3-2(x+3)
18 . 18x+3x-3=18-2(2x-1)
19 . 3(20-y)=6y-4(y-11)
20. -(x/4-1)=5
21. 3[4(5y-1)-8]=6
22.3X+189=521
23.4Y+119=22
24.3X*189=5
25.8Z/6=458
26.3X+77=59
27.4Y-6985=81
28.87X*13=5
29.7Z/93=41
30.15X+863-65X=54
31.58Y*55=27489
32.3X+18=52 x=34/3
33.4Y+11=22 y=11/4
34.3X*9=5 x=5/27
35.8Z/6=48 z=36
36.3X+7=59 x=52/3
37.4Y-69=81 y=75/4
38.8X*6=5 x=5/48
39.7Z/9=4 y=63/7
40.15X+8-5X=54 x=4.6
41.5Y*5=27 y=27/40
42.8x+2=10 x=1
43.x*8=88 x=11
44.y-90=1 y=91
45.2x-98=2 x=50
46.6x*6=12 x=1/3
47.5-6=5x x=-1/5
48.6*x=42 x=7
49.55-y=33 y=22
50.11*3x=60 x=20/11
51.8-y=2 y=-6
52.x+2=3
53.x+32=33
54.x+6=18
55.4+x=47
56.19-x=8
57.98-x=13
58.66-x=10
59.5x=10
60.3x=27
61.7x=7
62.8x=8
63.9x=9
64.10x=100
65.66x=660
66.7x=49
67.2x=4
68.3x=9
69.4x=16
70.5x=25
71.6x=36
72.8x=64
73.9x=81
74.10x=100
75.11x=121
76.12x=144
77.13x=169
78.14x=196
79.15x=225
80.16x=256
81.17x=289
82.18x=324
83.19x=361
84.20x=400
85.21x=441
86.22x=484
87.111x=12321
88.1111x=1234321
89.11111x=123454321
90.111111x=12345654321
91.46/x=23
92.64/x=8
93.99/x=11
94.1235467564x=0
95.2x+1= -2+x
96.4x-3(20-x)=3
.-2(x-1)=4
98.3X+189=521
99.4Y+119=22 5
100.3X+77=59
101.4Y-6985=81
102.X=0.1
103.5X=55.5
104.Y=50-85
105.3y-y=3+4,2y=7,y=3.5
106.0.4x+0.1x=2-3;0.5x=-1,x=-2
107.5x+15-2x-2=10,3x=-3,x=-1
108.[73X+78(100-X)]除以100=75.4
解:方程两边同乘以100,得73x+78(100-x)=7540
去括号,得 73x+7800-78x=7540
移项,得 73x-78x=7540-7800
合并同类项,得 -5x=-260
系数化为1,得 x=52
109.9x-120=5(x-8)
解这个方程,得 x=20
110.4x/5-30+10=3/4(x-10)
解这个方程,得 x=250
111.x+100=10x+1-414
解这个方程,得 x=57
112. x(1+20%)=9600
y(1-20%)=9600
解得 x=8000
y=12000
113.15(x-1)-8(3x+2)
=2-30(x-1)
21x=63
x=3
114.5x+4.5(103-x)=486
解得x=45
115.8-0.5x=4.5.
解这个方程,得x=7
116.180x=80x+80×5,
移项,得100x=400.
系数化为1,得x=4.
117.1.6+1+x+1=2(3-2×0.5)
解得x=0.4,
118.3x=9
119. 5x=110
120.7(5+6)-x=0
121.3x/5=45x
122.X-480-(X-480)×0.375=5/12 X
x-480-(3/8x-180)=5/12x
x-480-3/8x+180=5/12x
x-3/8x-5/12x=480-180
5/24x=300
x=1440
123.20x+30*2x+70*(47-3x)=2120
20x+60x+3290-210x=2120
3290-120x=2120
x=9
124.3X/5 +10= 10/7
125.2x+5=9
126.10x-5(15-x)=60
x=9
127.8x=6*40/60+8
x=3/2
128.20-X=5 X=15
129.7(2x-1)-3(4x-1)=4(3x+2)-1
解 14x-7-12x+3=12x+8-1
14x-12x-12x=8-1+7-3 -10x=11 x=-1
130.2(x-2)+2=x+1
131.2(x-2)-3(4x-1)=9(1-x)
132.11x+64-2x=100-9x
133.7(2x-1)-3*(4x-1)=4(3x+2)-1
134.(5x+1)+(1-x)=(9x+1)+(1-3x)
135.(x-6)*7=2x
136.x+(4/5)x-30=x-10+(3/4)(x-10)
137.x-x/4=x-72
138.1800=60[x-(30-x)]
139.14.59+x-25.31=0
x=10.72
140.x-48.32+78.51=80
x=49.81
141.820-16x=45.5×8
x=28.5
142.(x-6)×7=2x
x=8.4
143.3x+x=18
x=4.5
144.0.8x+2.2=6.6
x= 11
145.12.5-3x=6.5
x=2
146.1.2(x-0.64)=0.54
x=1.09
147.x+12.5=3.5x
x=5
148.8x-22.8=1.2
x=3
149.[(x-140)*0.57+140*0.43]/x=0.5
0.57x-79.8+60.2=0.5x
0.07x=19.6
x=280
150.(X+22)/(8X-22)=2/5
5*(X+22)=2*(8X-22)
5X+110=16X-44
11X=154
X=14
151.90%*(1+x%)=1
解得: x=1/9
152.(1-10%)X+(1+5%)(100-X)=100(1+2%)
结果X=20元
153.X+4/5X-30=X-10+3/4(X-10)
X=250
154.x-(x/4)=x-72
x=288
155.180*2=60[X-(30-X)]
X=18
156.1-X/3=2[1-3X/8]
X=2.4
157.0.4(x-0.2)+1.5=0.7x-0.38
x=6
158.30x-10(10-x)=100
x=5
159.4(x+2)=5(x-2)
x=18
160.120-4(x+5)=25
x=18.75
161.15x+863-65x=54
x=16.18
162.3(x-2)+1=x-(2x-1)
x=3/2
163.11x+64-2x=100-9x
x=2
164.5x+6+x=12 x=2
165.3y+(9-6)=33 y=10
166.3x+20=4x-25 x=45
167.6x+6(x-2000)=150000 x=13500
我终于知道为什么么有人帮你找了呀,实在是忒辛苦了点,本来想趁么事情做就帮你找了一点,么想到,等我找完才发现,我花了整整3个小时,惊人的数字呀,我还得帮你编号编好.格子排好,看不清的字重新帮你打一遍,哥们啊,你姐姐我这么帮你,多多感谢我呀
虽然不盼望起什么大作用,但应该还是对你有些帮助,自己保重吧
对了,我也初中,扣扣752591704
数学我也蛮感兴趣滴.有啥问题口以问我哈,我也可以增长见识
声明:本站所有文章资源内容,如无特殊说明或标注,均为采集网络资源。如若本站内容侵犯了原著者的合法权益,可联系本站删除。